MONET

What:

Monet simulates the flight of several thousand electrons through the silicon lattice and follows them individually as they drift in the electric field, then scatter with phonons, impurities or boundaries, and so on. This is a semi-classical approach because the scattering rates are computed quantum-mechanically (from Fermi's Golden Rule using wave function overlap integrals) yet during the free flight between scattering events the particles simply follow Newton's Laws (F=ma). The method is called Monte Carlo (MC) because of the stochastic nature in which the scattering events are simulated: a random number is drawn and compared with a scattering probability, then the scattering event is chosen based on this comparison.

Download:

source code (in C) with three examples and user manual. [4Mb zip file]

How:

One key ingredient in all such MC codes is the electron band model. Monet uses analytic, non-parabolic bands. This is both easier to implement and faster -- and it is a reasonable approximation for simulating electron transport in devices with operating voltages below the band gap (1.1 V in silicon), such as future nanoelectronic devices. Full-band simulators are mainly needed to resolve impact ionization and high band structure transport details. Consequently Monet ignores sub-band gap impact ionization. Here's a short summary of Monet's main features:

• analytic bands (non-parabolicity 0.5 eV^-1)
• scattering with six intervalley phonons
• separate scattering with intravalley LA and TA phonons
• phonon dispersion used both for acoustic and optical phonon scattering
• new empirical set of phonon scattering potentials, in better agreement with recent ab initio calculations and strained silicon mobility data

One of the features that distinguish Monet from other analytic-band MC codes is that all phonon generation and absorption events are tallied. Hence, very detailed heat generation statistics can be gathered. The simulation can be run in a constant E-field to obtain velocity-field curves, electron mobilities or the basic phonon distributions at the given E-field -- or in 1- or 2-D with periodic boundary conditions on an E-field grid extracted from another device simulator like Medici. Monet does not solve the Poisson equation (this is also known as Monte Carlo in the "frozen field" approximation). The total amount of charge inside the device is given by the previous device simulator and only two device contacts can be included. This implies that electrons exiting the device through one contact are immediately injected at the other contact with thermally distributed energies and randomly oriented velocity components.

Another feature of Monet is its treatment of acoustic intravalley scattering. Scattering with LA and TA phonons is treated separately and the full phonon dispersion is used when calculating the acoustic intravalley scattering rates. The LA/TA scattering deformation potentials are derived from the most recent values of the shear and dilatation potentials available in the literature. Other analytic-band MC codes group LA and TA scattering together and assume a single phonon velocity, i.e. no phonon dispersion.

The following figures illustrate the silicon band diagrams:

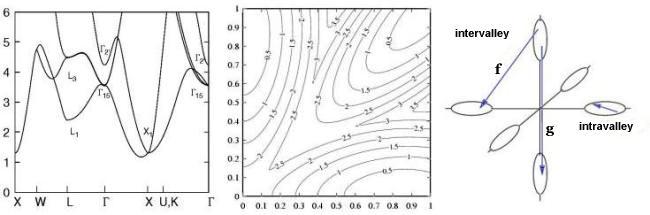
The figure on the left (courtesy IBM) shows the full conduction band diagram. The middle figure (courtesy C. Jungemann) shows constant energy contours near the bottom of the conduction band (notice the ellipsoidal shape around the minima at 0.85). The third figure shows the ellipsoidal energy pockets "inhabited" by conduction band electrons in an analytic-band MC code like Monet, and the possible phonon scattering transitions.

---

updated Jul 2007